卷积神经网络

深度学习目前在各个领域，尤其是图像和语音领域上，表现远超传统方法，靠的是卷积神经网络这个特殊的神经网络，卷积神经网络和普通神经网络的区别主要在于其深度以及特殊的层上，而其核心的层则是卷积层和池化层。

卷积层

卷积层采用类似卷积的方式，对于一个三维的数据体（C×H×W），卷积操作使用一个感知窗口（C×F×F）去遍历扫描数据（其中F为一个很小的数，比如7或3），移动窗口下的数据和感知窗口的权重进行点乘，再加上一个偏置形成下一层的一个神经元。这么做的好处是局部感知和参数共享:

• 局部感知：下一层的一个神经元只和上一层的神经元的一个子集相关
• 参数共享：每一个feature map中的神经元共享一套感知窗口参数

输入

4维数据体，存储顺序一般用NCHW表示，N为batch size，C为channel size，H和W分别为高和宽。

超参数

• filter 感知场（receptive field）的大小，通常用F表示
• stride filter 的移动步长，通常用S表示
• padding 图像边缘补0的大小，通常用P表示
• K 输出特征的个数/channel

对于每一个输出特征，卷积层的可训练参数是$F*F*C + 1$，因此，对于K个输出特征，总共的可训练参数是$K*(F*F*C + 1)$

输出数据体的维度计算

对于输入数据体NCHW，输出数据体的维度计算如下：
$$
\begin{align}
& N^{‘} = N \\
& C^{‘} = K \\
& H^{‘} = (H - F + 2 \times P) / S + 1 \\
& W^{‘} = (W - F + 2 \times P) / S + 1 \\
\end{align}
$$

卷积层的前向计算

假设 batch size 为1，首先我们知道卷积层的权重矩阵是$\text {kernal_size} \times \text {number_of_kernels}$,其中$\text {number_of_kernels} = K$，$\text {kernal_size} = C \times F \times F$。这个矩阵的每一列都是一个kernal。

这个权重矩阵里的每一列需要和输入图像的每一个小区域相乘，获得输出特征的每一个神经元，因此，需要把输入图像的每一个小区域（3维数据体）拉伸成一行，所有的这些行就可以组成一个大矩阵，然后用权重和这个大矩阵相乘就可以得出最后的输出，这个大矩阵的维度是 $\text {number_of_patchs} \times \text {kernal_size}$，其中$\text {number_of_patchs} = H^{‘} \times W^{‘}$，即小区域的总个数是输出图像包含的神经元总数。

因此，这两个矩阵相乘可以得到一个$\text {number_of_patchs} \times \text {number_of_kernels}$的矩阵，这个矩阵的每一列然后再加上一个大小为K的偏置就是最后的输出。
对于batch size 大于1的情况，只需要循环进行上述操作即可，batch中的每一个图像的计算是独立的。

在caffe2中的实现的函数如下：

auto f = [&](Tensor<Context>* col_buffer) {
    // col_buffer 存放的是每一个小区域按行堆叠得到的矩阵，总大小是 number_of_patchs * kernal_size
    col_buffer->Resize(buffer_shape);
    T* col_buffer_data = col_buffer->template mutable_data<T>();
    // Im2col, followed by gemm.
    for (int image_id = 0; image_id < N; ++image_id) {
      // 对于每一个图像
      for (int group_id = 0; group_id < group_; ++group_id) {
        // 指定group的卷积操作会选择特定数据的上层特征进行卷积计算，这里为了便于理解可以认为group_id 为0，即不进行 group convolution
        if (kernel_.size() == 2) {
          // 把图片拉直存入col_buffer_data
          math::Im2col<T, Context, StorageOrder::NCHW>(
              Xdata + group_id * input_offset,
              C / group_,
              input_dims[0],
              input_dims[1],
              kernel_h(),
              kernel_w(),
              dilation_h(),
              dilation_w(),
              pad_t(),
              pad_l(),
              pad_b(),
              pad_r(),
              stride_h(),
              stride_w(),
              col_buffer_data,
              &context_);
        } else {
          math::Im2colNd<T, Context, StorageOrder::NCHW>(
              Xdata + group_id * input_offset,
              img_shape_device_.template data<int>(),
              col_buffer_shape_device_.template data<int>(),
              C * input_image_size,
              col_buffer_size,
              kernel_device_.template data<int>(),
              stride_device_.template data<int>(),
              dilation_device_.template data<int>(),
              pads_device_.template data<int>(),
              kernel_.size(),
              col_buffer_data,
              &context_);
        }
        // Weight term: 乘以权重矩阵，存入Ydata
        math::Gemm<T, Context>(
            CblasNoTrans,
            CblasNoTrans,
            M / group_,
            output_image_size,
            kernel_dim,
            1,
            filter.template data<T>() + group_id * filter_offset,
            col_buffer_data,
            0,
            Ydata + group_id * output_offset,
            &context_);
      }
      if (InputSize() == 3) {
        // Bias term can be carried out outside the group definition
        // to be efficient.
        // 添加偏置
        auto* bias_data = Input(BIAS).template data<T>();
        math::Gemm<T, Context>(
            CblasNoTrans,
            CblasNoTrans,
            M,
            output_image_size,
            1,
            1,
            bias_data,
            bias_multiplier_.template data<T>(),
            1,
            Ydata,
            &context_);
      }
      // 更新图像数据
      Xdata += input_offset * group_;
      Ydata += output_offset * group_;
    }
  };

卷积层的梯度计算

实际上卷积层的前向迭代实现的是一个矩阵与矩阵相乘的操作，即：
$$
Y = XW + B
$$
其中X就是把图像转成列矩阵得到的矩阵，W是权重矩阵，B是偏置矩阵，Y相对于X、W、B的导数是：
$$
\begin{align}
& \frac{dY}{X} = W \\
& \frac{dY}{M} = X \\
& \frac{dY}{B} = 1 \\
\end{align}
$$

池化层

MaxPooling？谁起的名字？功能就是从一个池子里选出最大的那个。四方形的池子。

输入

4维数据体，存储顺序一般用NCHW表示，N为batch size，C为channel size，H和W分别为高和宽。

超参数

• spatial extent, F（池子大小）

• stride, S（移动池子的步长）

注意到池化层并没有可训练的参数。

池化层的梯度计算

因为池化层没有可训练的参数，因此该层实际上是把上层传入的参数分配给下层的某个神经元（MaxPooling中选中的那个），因此在进行前向迭代时，会存储选中神经元的索引。

LeNet

LeNet是最早成功的卷积神经网络，用来识别手写字体和数字等，下面是这个网络的架构(红色椭圆是输入和输出的数据，蓝色矩形是功能层，或者叫对数据的操作子)：

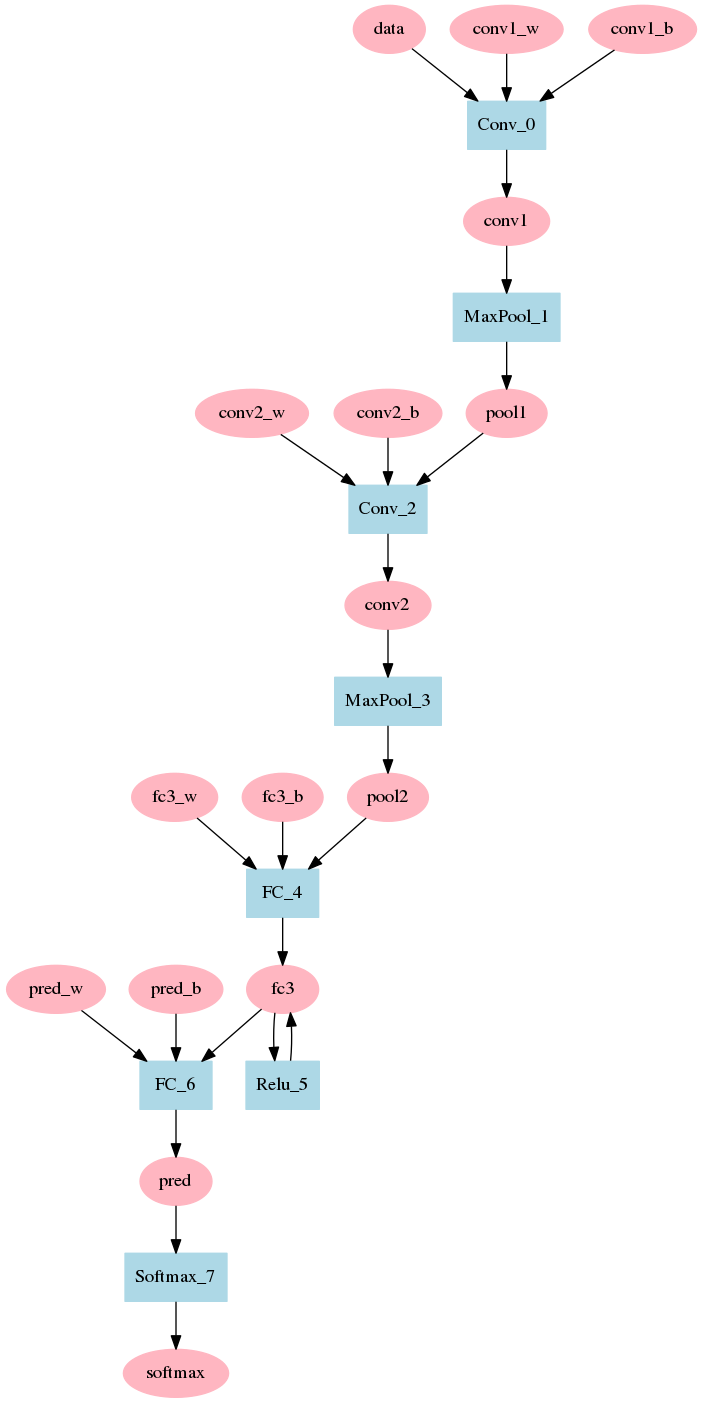
LeNet一共有8层，由两个卷积层加上两个直连层组成，其中每个卷积层之后都会跟一个MaxPooling池化层，第一个直连层后经过了ReLU激活层，第二个直连层的输出则直接输入到SoftMax层，最后得出网络的输出。